Deep Dive into Optimization Algorithms in Deep Learning

Optimization techniques are the backbone of successful deep learning model training, guiding the adjustment of model parameters for enhanced performance. Among these techniques, Gradient Descent (GD) serves as the fundamental building block, forming the basis for more advanced variants. This article delves into the nuances of Gradient descent and its derivatives, including Stochastic Gradient descent (SGD), Mini Batch Gradient descent, Momentum-based GD, and Nesterov Accelerated GD.

 Optimization in deep learning refers to the process of finding the best set of model parameters (weights and biases) that minimizes a given objective function, also known as the loss function or cost function. The objective of optimization is to train a deep neural network to make accurate predictions on the training data by adjusting its parameters during the learning process. In deep learning, optimization involves iteratively updating the model’s parameters using gradient-based optimization algorithms.

Main Gradient Descent variants are :

• Batch GD
• Stochastic GD
• Mini-batch GD

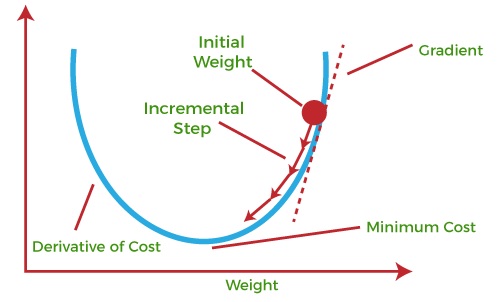
Gradient Descent:

Gradient descent is an iterative optimisation process for minimising a specified objective function (also known as the cost function or loss function) by altering the model’s parameters in the direction of a local or global minimum.

 It is an essential part in training many machine learning models, such as deep neural networks. The main principle underlying gradient descent is to take steps in the direction of the objective function’s steepest decline, which corresponds to the negative of the function’s gradient with respect to the model’s parameters. The method iteratively adjusts the parameters until the goal function reaches a minimal or satisfactory value, at which point the algorithm stops.

Batch Gradient Descent:

In Batch Gradient Descent, all the training data is taken into consideration to take a single step. We take the average of the gradients of all the training examples and then use that mean gradient to update our parameters. So that’s just one step of gradient descent in one epoch. Batch Gradient Descent is great for convex or relatively smooth error manifolds. In this case, we move somewhat directly towards an optimum solution.

Stochastic GD:

SGD addresses the computational inefficiency of traditional GD by updating the model’s parameters using only a single randomly selected training example in each iteration. This introduces significant variance in the updates, which can help escape local minima and converge faster. However, the noise introduced by single examples can also lead to erratic convergence.

As a result, SGD is much faster and more computationally efficient, but it has noise in the estimation of the gradient. Since it updates the weight frequently, it can lead to big oscillations, which makes the training process highly unstable.

Mini-batch SGD:

Mini-Batch Stochastic Gradient Descent strikes a balance between the efficiency of GD and the variance of SGD. It divides the dataset into smaller batches (mini-batches) and computes the gradient using the average gradient over a batch. This approach leverages the benefits of vectorized operations in modern hardware, leading to faster convergence while reducing the noise compared to pure SGD.

The update of Mini-batch SGD is much noisy compared to the update of the GD algorithm. It can take a longer time to converge than the GD algorithm and may get stuck at local minima. But there is less time complexity to converge compared to standard SGD algorithm.

SGD with Momentum:

Stochastic Gradient Descent (SGD) with momentum is an optimization algorithm that incorporates the concept of momentum to accelerate the parameter updates during training. It is an extension of the basic SGD algorithm and aims to address the challenges associated with oscillations and slow convergence in the standard SGD. In standard SGD, the parameter updates at each iteration are solely determined by the current gradient of the loss function with respect to the model parameters. This can lead to noisy and oscillatory updates, especially in scenarios with irregular or noisy gradients. The momentum term, introduced in SGD with momentum, helps to smooth out these oscillations and provide a sense of inertia during optimization.

Nesterov Accelerated Gradient (NAG):

Nesterov Accelerated GD, often referred to as Nesterov Momentum or NAG, is an improvement upon the standard momentum-based approach. It calculates the gradient not at the current parameter values but at an estimate of the future position of the parameters. This “look-ahead” feature allows the algorithm to anticipate its next move and results in more precise updates, often leading to faster convergence.

In the case of SGD with a momentum algorithm, the momentum and gradient are computed on the previous updated weight. Momentum may be a good method but if the momentum is too high the algorithm may miss the local minima and may continue to rise up. So, to resolve this issue the NAG algorithm was developed. It is a look ahead method.

Choosing The Right Algorithm:

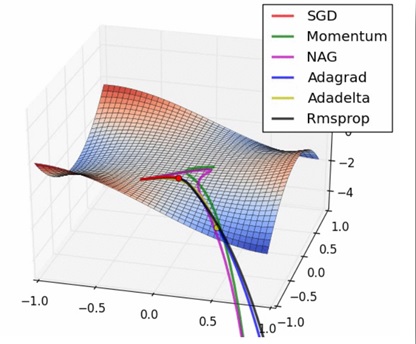
Selecting the appropriate optimization algorithm depends on several factors, including the dataset size, model architecture, and convergence speed required. As a rule of thumb, for large datasets, Mini-Batch GD, along with momentum-based techniques like Nesterov Accelerated GD, tends to work well. For smaller datasets, traditional GD or even SGD might suffice.In practice, it’s common to experiment with different optimization algorithms, learning rates, and other hyperparameters to identify the combination that yields the best results for a specific problem.

Conclusion: Optimization algorithms lie at the heart of training deep learning models. From the foundational Gradient Descent to the advanced Momentum-based GD and Nesterov Accelerated GD, each algorithm comes with its strengths and weaknesses. Understanding these algorithms and their nuances is essential for effectively training neural networks and achieving superior performance on a wide range of tasks.