Multi-Layer Perceptron Networks
May 4, 2024Exploring Multi-Layer Perceptron Networks: Understanding, Architecture, Applications, and Future Directions
In the ever-evolving landscape of Artificial Intelligence (AI) and Machine Learning, Multi-Layer Perceptrons (MLPs) stand out as a fundamental building block for understanding complex Neural Network models. This article delves into the realms of MLPs, explaining their architecture, functionality, diverse applications, and the challenges they face in the broader context of AI development.
Understanding Multi-Layer Perceptrons
A Multi-Layer Perceptron (MLP) is a class of feedforward Artificial Neural Network (ANN). It consists of at least three layers of nodes: an input layer, one or more hidden layers, and an output layer. Each node, except for the input nodes, is a neuron that uses a nonlinear activation function. MLPs are distinguished from other Neural Networks by their deep structure and their ability to approximate virtually any continuous function, a theoretical property known as the universal approximation theorem.
Architecture of MLPs
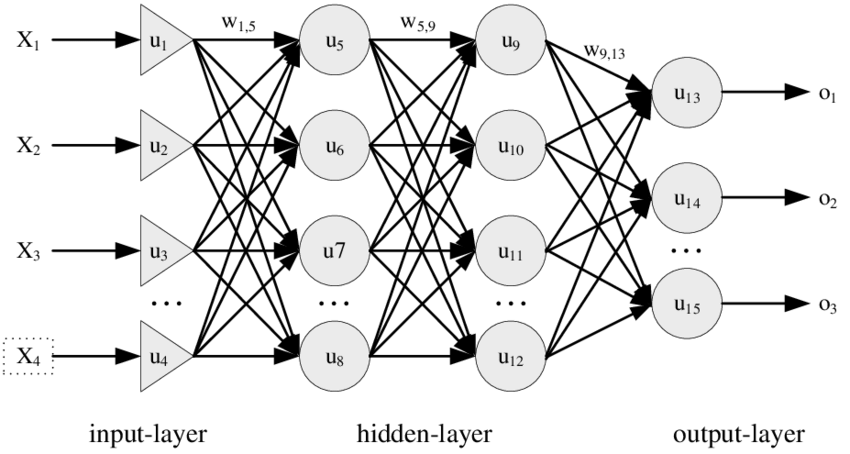
Input Layer:
The input layer is the starting point in an MLP architecture. It consists of neurons equal to the number of features in the dataset. Each neuron in this layer directly receives a single feature from the input data, acting merely as a passive input receiver that passes the data to the next layer without performing any computation.
Hidden Layers:
The hidden layers are where most of the computation in an MLP takes place. Each layer is composed of numerous neurons, and each neuron in a hidden layer performs several steps of processing:
Linear Combination:
First, each neuron computes a weighted sum of its inputs. The inputs to a hidden layer neuron come from either the input layer or the previous hidden layer’s output. Each input has an associated weight, and the neuron also has a bias term. The formula being
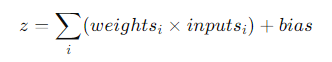
Activation Function:
After computing the linear combination, the result is passed through an activation function. The purpose of the activation function is to introduce non-linearity into the model, allowing it to learn more complex patterns. Common activation functions include ReLU (Rectified Linear Unit), which is used for hidden layers due to its computational efficiency and ability to reduce the likelihood of vanishing gradients, and the sigmoid or tanh functions, which were traditionally more common.
Output Layer:
The final layer of an MLP is the output layer, which formats the output of the network to be suitable for the task at hand (e.g., one node for binary classification, multiple nodes for multiclass classification, or a single node for regression). This layer also includes an activation function appropriate for the specific type of output required:
- For binary classification tasks, a sigmoid activation function might be used to squish the output between 0 and 1, representing the probability of the input belonging to the positive class.
- For multiclass classification, a softmax activation function can be used to convert the outputs to probabilities that sum to one, representing the likelihood of each class.
- For regression tasks, typically no activation function or a linear activation function is used, allowing the network to output a range of values.
Learning Mechanism:
MLPs learn by adjusting the weights and biases to minimize the difference between the predicted output and the actual target values. This is typically done using backpropagation, a method of calculating gradients of the error function with respect to each weight and bias in the network, followed by an optimization algorithm like stochastic gradient descent to make small adjustments to the weights and biases.

Architecture of Multi-Level Perceptron Networks
Key Principles of MLPs
- Layered Structure: MLPs are composed of multiple layers through which data flows in a forward direction. Each layer’s output is the subsequent layer’s input, culminating in a prediction at the output layer.
- Weight and Bias: Every neuron in a Neural Network has its associated weights and biases, which are adjusted during the training process to minimize the error in prediction. The backpropagation algorithm, along with an optimization method such as gradient descent, is typically used to update these parameters.
- Activation Function: Activation functions introduce nonlinear properties to the Network, enabling it to learn complex patterns. Without nonlinearity, even with many layers, the MLP would still behave like a single-layer perceptron.
Impact and Applications
- MLPs have wide-ranging applications across various sectors:
- Finance: For credit scoring, algorithmic trading, and risk management.
- Healthcare: MLPs help in disease diagnosis, personalized medicine, and medical image analysis.
- Technology: They are used in speech recognition systems, customer service bots, and real-time translation tools.
- Marketing: MLPs analyze consumer behavior, predict churn, and enhance customer segmentation.
Challenges in MLPs
Despite their versatility, MLPs face several challenges:
- Overfitting: MLPs with many layers and neurons can overfit the training data, learning details and noise that do not generalize to new data.
- Computationally Intensive: Training deep MLPs requires significant computational resources, especially as data volume and model size increase.
- Vanishing Gradients: In deep Networks, gradients can become very small, effectively stopping the Network from learning. Advanced techniques like batch normalization or different activation functions are needed to mitigate this.
The Path Forward
The future of MLPs in AI is tied to ongoing research and development. Innovations such as dropout, advanced regularization techniques, and novel optimization algorithms are enhancing MLPs’ efficiency and applicability. Furthermore, integration with other Neural Network architectures, like Convolutional Neural Networks (CNNs) and Recurrent Neural Networks (RNNs), is expanding the horizons of what MLPs can achieve.
In conclusion, Multi-Layer Perceptrons are a cornerstone of modern Neural Network architectures, offering a blend of simplicity and power that makes them integral to the AI toolkit. As research progresses, the potential for MLPs to contribute to more robust, efficient, and intelligent systems is boundless, promising exciting advancements in AI capabilities.

Implementation of multilayer perceptron Network