Unlocking Insights with Linear Regression: A Fundamental Tool in Data Analysis
May 4, 2024Within the broad field of data analysis and machine learning, linear regression is a key method for comprehending and forecasting correlations between variables. It is a vital tool in the toolbox of a data scientist, useful in fields ranging from marketing to engineering and from economics to healthcare. Its simplicity and interpretability make it easy to use. We will examine linear regression’s definition, methodology, underlying presumptions, and real-world applications in this post.
- Understanding Linear Regression
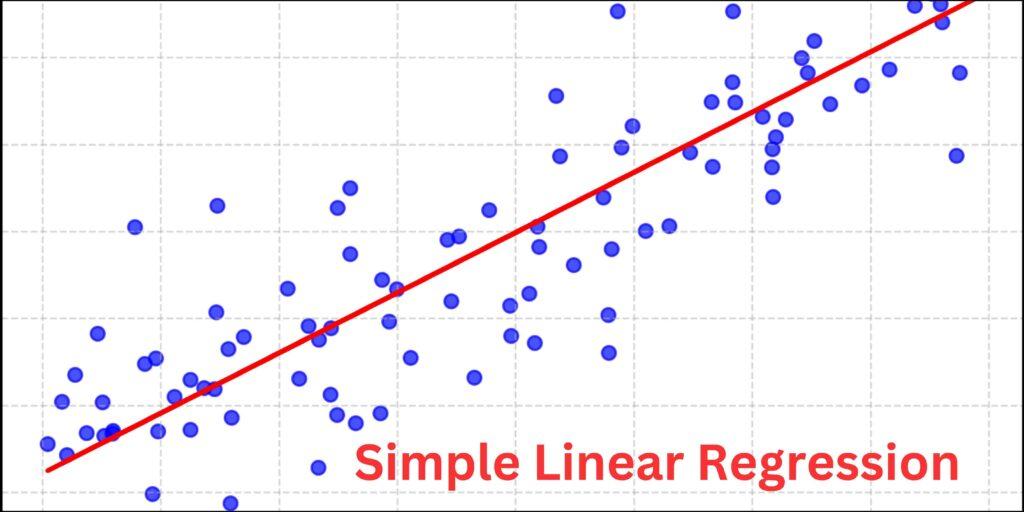
Fundamentally, a linear regression is a statistical technique that models the relationship between one or more independent variables, usually represented by the letter (X), and a dependent variable, usually represented by the symbol (Y). It is expected that the relationship is linear, i.e., that changes in the independent variable(s) cause proportionate changes in the dependent variable.
Y=β0+β1X+ϵ
Where:
- The dependent variable is Y.
- The independent variable is X.
- The intercept, or the value of Y when X is 0, is denoted by β0.
- The slope, or the change in Y for a unit change in X, is denoted by β1.
- The error term, denoted by ϵ, quantifies the discrepancy between the actual and anticipated values of Y
- How Does Linear Regression Work?
The Finding the coefficients (β0 and β1) that minimize the sum of squared differences between the dependent variable’s anticipated and actual values is the main objective of linear regression. The least squares method, in which the coefficients are selected to minimize the residual sum of squares (RSS), is frequently used to accomplish this process. To put it simply, linear regression minimizes the total distance between the observed data points and the line in order to determine which line best fits the data.
- Assumptions of Linear Regression
Even though linear regression is an effective technique, understanding its underlying assumptions is crucial to guaranteeing the accuracy of the model’s output:
1. Linearity: It is considered that there is a linear relationship between the independent and dependent variables.
2. Independence: The disparities between the observed and projected values, or residuals, are unrelated to one another.
3. Homoscedasticity: At every level of the independent variables, the residuals’ variance remains constant.
4. Normality: The residual distribution is normal.
5. No Multicollinearity: When there are numerous independent variables in a multiple linear regression, the variables shouldn’t have a strong correlation with one another.
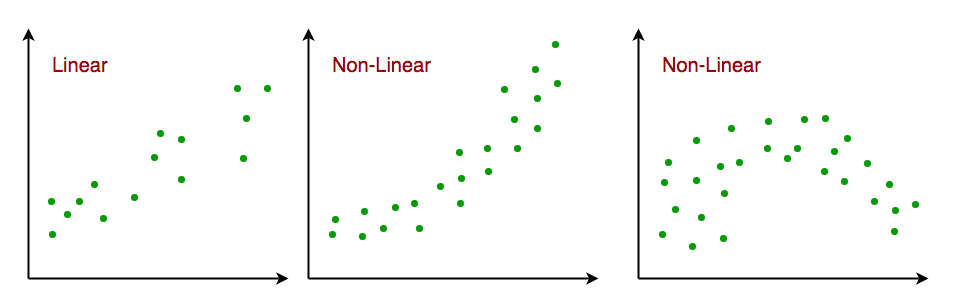
The significance of performing diagnostic checks prior to depending on the outcomes of a linear regression model is highlighted by the possibility that violations of these presumptions could result in skewed estimations and incorrect forecasts.
- Practical Applications
Linear regression finds applications in a wide range of fields:
1. Economics: Estimating the cost of a home by taking into account variables like location, size, and number of bedrooms.
2. Marketing: Calculating sales by taking into account pricing, advertising spend, and other market factors.
3. Healthcare: Forecasting patient results by utilizing treatment plans, medical histories, and demographic data.
4. Engineering: Examining how manufacturing process performance measurements and input parameters relate to one another.
Apart from its predictive capabilities, linear regression is an invaluable tool for comprehending the magnitude and orientation of associations among variables, pinpointing significant elements, and arriving at informed conclusions based on empirical evidence.

- Conclusion
A fundamental tool in data analysis, linear regression offers a straightforward but effective framework for simulating connections between variables. For academics, analysts, and practitioners in a variety of fields, its interpretability and adaptability make it a vital tool. Data professionals can drive educated decision-making in a data-driven world and unlock significant insights by comprehending its principles, assumptions, and applications.