Support Vector Machine (SVM)
May 4, 2024Support Vector Machine (SVM) is a powerful supervised learning algorithm used for both classification and regression. The goal of the SVM algorithm is to create the best line or decision boundary that can segregate n-dimensional space into classes so that we can easily put the new data point in the correct category in the future. This best decision boundary is called a hyperplane. SVM chooses the extreme points/vectors that help in creating the hyperplane. These extreme cases are called as support vectors, and hence algorithm is termed as Support Vector Machine.
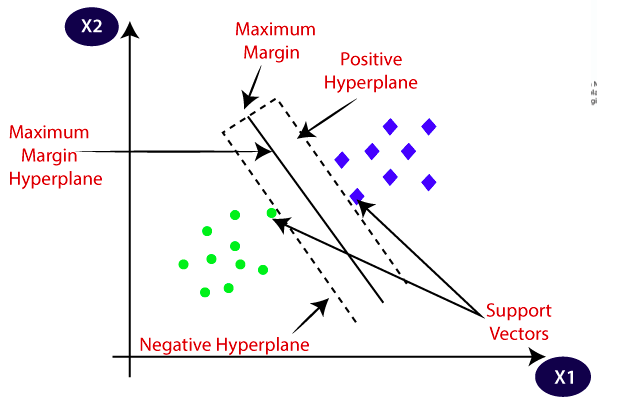
- Hyperplane:
There can be multiple lines/decision boundaries to segregate the classes in n-dimensional space, but we need to find out the best decision boundary that helps to classify the data points. This best boundary is known as the hyperplane of SVM
- Support Vectors:
The data points or vectors that are the closest to the hyperplane and which affect the position of the hyperplane are termed as Support Vector. Since these vectors support the hyperplane, hence called a Support vector.

Working principle of SVM regression
The working principle of SVM regression lies in finding the hyperplane that minimizes the error, known as the epsilon-insensitive tube, which contains the majority of the training data points. By adjusting the slack variable and the tube width, SVM regression adapts to the data distribution and effectively captures the underlying patterns. We will explore the mathematical formulation and underlying concepts that govern the working of SVM regression in this section.
Tuning parameters for SVM regression
Effective tuning of parameters is crucial for enhancing the performance of SVM regression. Parameters such as the choice of kernel, the regularization parameter (C), and the kernel-specific parameters significantly impact the model’s accuracy and robustness. Through meticulous parameter tuning, the model can capture intricate patterns and generalize well to unseen data. This section will delve into the various parameters and their influence on SVM regression’s performance.
Evaluating the performance of SVM regression
Performance evaluation is essential for assessing the efficacy of SVM regression models. Metrics such as Mean Squared Error (MSE), R-squared, and cross-validation scores provide insights into the model’s predictive capabilities and generalization to new data. Additionally, visualizations like learning curves and residual plots offer a comprehensive understanding of the model’s strengths and potential areas of improvement. This section will thoroughly explore the techniques and metrics used to evaluate SVM regression performance.
SVM can be of two types:
- Linear SVM:
Linear SVM is used for linearly separable data, which means if a dataset can be classified into two classes by using a single straight line, then such data is termed as linearly separable data, and classifier is used called as Linear SVM classifier.
- Non-linear SVM:
Non-Linear SVM is used for non-linearly separated data, which means if a dataset cannot be classified by using a straight line, then such data is termed as non-linear data and classifier used is called as Non-linear SVM classifier.
Advantages and limitations of SVM regression
Advantages
SVM regression exhibits robustness to overfitting, handles high-dimensional data effectively, and can capture complex relationships between variables.
Limitations
On the downside, SVM regression can be computationally intensive, sensitive to the choice of kernel, and may require careful parameter tuning.
Conclusion and future prospects
In conclusion, SVM regression offers a powerful approach to modeling the relationship between input and output variables in the context of machine learning. Its robustness, flexibility, and ability to handle non-linear relationships make it a valuable tool for regression tasks. Looking ahead, advancements in kernel techniques, parallel computing, and optimization algorithms hold promise for further enhancing the scalability and efficacy of SVM regression. This brings optimism for its continued evolution and widespread application in diverse domains.